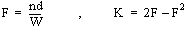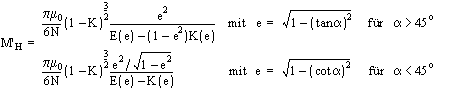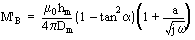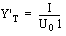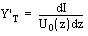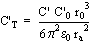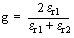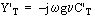Einleitung
Die Zuverlässigkeit
ausgedehnter Automatisierungs- oder Kommunikationssysteme ist ein Thema
von zunehmender Bedeutung. Die Zuverlässigkeit kann durch in Kabel
eingekoppelte Störungen beeinträchtigt werden. Speziell in frühen
Planungsstadien solcher Systeme ist es erforderlich, mittels einer Simulation
die zu erwartenden Störströme und Störspannungen zu berechnen.
Zur Durchführung einer solchen Berechnung müssen neben den primären
Leitungsbelägen R', L', C' und G' der betrachteten Leitungen im Fall
von geschirmten Leitungen deren komplexe Transferimpedanz und Transferadmittanz
bekannt sein. Besonders bei Mehrfachleiterkabeln ist die Bestimmung der
Transferimpedanzen und Transferadmittanzen der einzelnen Innenleiter über
theoretische Berechnungen noch immer problematisch, so daß die Bestimmung
der genannten Parameter über Messungen erfolgen muß.
Definition der komplexen Transferimpedanz
Sobald sich ein geschirmtes
Kabel in einer Umgebung befindet, in der z.B. durch Feldeinfall oder andere
Interferenzphänomene ein Störstrom auf den Kabelschirm eingespeist
wird, hat dieser Störstrom eine Störspannung auf dem (den) Innenleiter(n)
des Kabels zur Folge. Die diese Einkopplung beschreibende Größe
ist die Transferimpedanz Z'
T . Die Transferimpedanz
eines Koaxialkabels ist als längengezogene, komplexe Größe
definiert als das Verhältnis der Störspannung auf dem Innenleiter
U zu dem Störstrom auf dem Kabelschirm I
0 .
Die Transferimpedanz
ist somit ein Gütemaßstab für den Kabelschirm. Je geringer
die Transferimpedanz ist, desto besser ist die Schirmwirkung des Kabelschirms.
Da der Schirmstrom keine Größe ist, deren Definition von der
Umgebung des Kabels abhängt, stellt die Transferimpedanz eine reine
Kabelkenngröße dar.
Schematische Darstellung
zur Definition der Transferimpedanz
Das dargestellte Spannungsmeßgerät
sollte ideal sein, d.h. über einen unendlichen Innenwiderstand verfügen,
um zu verhindern, daß die Spannungsmessung durch einen auf dem Innenleiter
fließenden Strom verfälscht wird.
Die Definition von Z' T ist
weiterhin nur für einen über die Leitungslänge konstanten
Störstrom gültig. Die im Bild gezeigte Leitung muß also
elektrisch kurz sein. Dies bedeutet, daß die Wellenlänge des
Störstromes I 0 wesentlich größer als
die Leitungslänge l sein muß.
Um die Transferimpedanz
in die Leitungstheorie integrieren zu können, ist es notwendig, sie
als differentielle Größe zu definieren
Auch hier gilt, daß
der auf dem Innenleiter fließende Strom Null sein muß.
Die physikalischen Einkopplungsmechanismen,
die zur Entstehung der Störspannung auf dem Innenleiter führen,
und in den folgenden Abschnitten näher erläutert werden, sind:
- Die Diffusionskopplung,
die als frequenzabhängige Änderung des elektrischen Feldes längs
der Innenseite des Kabelschirms beschrieben werden kann.
- Die Aperturkopplung,
die den Durchgriff des magnetischen Feldes des Störstroms durch Öffnungen
im Kabelschirm beschreibt.
- Die Geflechtkopplung,
die nur bei Kabeln mit einem Geflechtschirm auftritt und ebenfalls als
magnetische Kopplung wirkt.
In der Literatur existiert
eine Vielzahl von Modellen, die diese Einkopplungsmechanismen mit den geometrischen
und elektrischen Eigenschaften des Kabelschirms verknüpfen und so
die Transferimpedanz als Funktion der Eigenschaften des Kabelschirms darstellen.
Bisher ist allerdings kein vollständig analytisches Modell bekannt,
das sowohl alle Einkopplungsmechanismen berücksichtigt, als auch meßtechnisch
über einen größeren Frequenzbereich verifiziert wurde.
Dies gilt insbesondere für den Phasenverlauf der Transferimpedanz.
Weiterhin wird die Transferimpedanz
als Superposition der Wirkungen der Einkopplungsmechanismen
aufgefaßt, wobei
der Term D'
T die Diffusionskopplung, der Term M'
H
die Aperturkopplung und der Term M'
B die Geflechtkopplung
beschreibt.
Diffusionskopplung
Zur Betrachtung der
Diffusionskopplung wird der Geflechtschirm eines Koaxialkabels vereinfachend
als homogener Hohlzylinder bzw. Rohr konstanten Querschnitts und konstanter
Wandstärke angenommen. Da beim Hohlzylinder Apertur- und Geflechtkopplung
nicht auftreten können, wird die Transferimpedanz lediglich durch
den Term D'
T ausgedrückt. Im Bild wird der Hohlzylinder
durch den Außenradius r
a und die Wandstärke
d beschrieben. Das Material besitzt die spezifische Leitfähigkeit
k
und die Permeabilität
m .
Aus einem massiven Hohlzylinder
bestehender Kabelschirm
Im Fall eines Gleichstroms
als Störstrom I
0 ergibt sich eine Transferimpedanz,
die dem Gleichstromwiderstandsbelag des Hohlzylinders R'
DC
entspricht.
Bekanntermaßen
erfolgt bei steigender Frequenz des Störstroms durch die Selbstinduktion
im Leiter eine Verdrängung des Stromes zur Außenseite des Hohlzylinders
hin. Dieser auch als Skin-Effekt bezeichnete Mechanismus wird durch die
äquivalente Leitschichtdicke
d charakterisiert,
die auch als Skin-Eindringtiefe bezeichnet wird.
Die Skin-Eindringtiefe
gibt an, in welcher Entfernung von der Oberfläche eines stromdurchflossenen
Leiters die Stromdichte auf den 1/e-ten Teil des Oberflächenwertes
abgesunken ist.
Die Transferimpedanz
eines homogenen Hohlzylinders, bei dem lediglich die Diffusionskopplung,
also nur der Term D'
T , einen Beitrag liefert, ist:
Der Betrag des Diffusionsterms
nimmt mit steigender Frequenz ab, sobald die Skin-Eindringtiefe die Wandstärke
unterschreitet. Das Bild zeigt den berechneten Verlauf von D'
T
,
der zur besseren Darstellung auf 1
W
/m normiert ist, für einen Kupfer-Hohlzylinder einer Wandstärke
von 0.1 mm.
Berechneter Verlauf von
D' T , normiert auf 1 W
/m, mit m = m
0
, k =56 . 10 6 S/m
und d=0.1 mm
Aperturkopplung
Befinden sich Aperturen
im Kabelschirm, was bei Kabeln mit Geflechtschirm der Fall ist, kann das
von dem auf dem Kabelschirm fließenden Störstrom herrührende
Magnetfeld durch die Aperturen in das Innere des Kabels hindurchgreifen.
Das Bild zeigt schematisch die durch die Apertur hindurchgreifenden Magnetfeldlinien,
die in zwischen dem Innenleiter des Koaxialkabels und der Innenseite des
Kabelschirms eine Störspannung U
s induzieren.
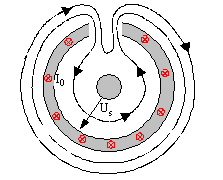
Magnetfelddurchgriff durch
eine Apertur im Kabelschirm nach
Bei einer kreisförmigen
Apertur ergibt sich unter der Voraussetzung, daß die Wellenlänge
des Störwechselstroms I
0 groß gegenüber dem Radius
der Apertur r
0 ist und die Dicke des Kabelschirms gegenüber
dem Kabeldurchmesser D vernachlässigt werden kann, nach die Gegeninduktivität
der Apertur M
12 als:
wobei U
s
=j
w M
12 I
0
gilt. Somit entspricht M
12 als längenbezogene Größe
M'
12 =M
12 /l dem Term M'
H
.
Für
n Aperturen pro Längeneinheit
gilt also M'
H =
n
M'
12 . Da die Gegeninduktivität der Aperturen kubisch
mit dem Aperturradius wächst, ist zu erkennen, daß es bei einer
gegebenen Gesamtfläche aller Aperturen eines betrachteten Kabelabschnittes
günstiger ist, wenn eine große Anzahl Aperturen geringen Radiuses
vorhanden ist, als wenn eine geringe Anzahl Aperturen eines größeren
Radiuses vorhanden wäre.
Ein Geflechtschirm,
wie er im Bild schematisch dargestellt ist, besitzt rhombusförmige
Aperturen. Mit dem Durchmesser einer einzelnen Geflechtlitze d, der Anzahl
von Litzen pro Flechtgruppe n, der Gesamtanzahl aller Flechtgruppen N,
der Breite, die eine Flechtgruppe zusammen mit der Apertur einnimmt W und
dem Flechtwinkel
a kann nach zunächst
der Füllfaktor F und die optische Bedeckung K berechnet werden:
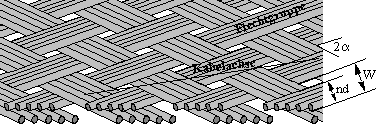
Schematische Darstellung
eines Geflechtschirms
Weiterhin wird kann
eine Näherungslösung für M'
H , die den
Winkel der rhombusförmigen Aperturen gegenüber der Kabelachse
berücksichtigt und die Rhombenform durch eine Ellipse approximiert,
angegeben werden:
K(e) und E(e) stellen
hierbei die bestimmten elliptischen Integrale erster und zweiter Gattung
in der Legendreschen Normalform F(e,
p
/2) und E(e,
p /2) dar.
Geflechtkopplung
Bei einem Geflechtschirm
befinden sich die Litzen einer Flechtgruppe auf einem Abschnitt des Kabels
auf der Außenseite des Schirms und auf einem folgenden Abschnitt
auf der Innenseite des Schirms. Die aus dieser geometrischen Besonderheit
des Geflechtschirms resultierende Störeinkopplung auf die Innenleiter
wird als Geflechtkopplung, in der englischsprachigen Literatur auch porpoising
(effect)" genannt, bezeichnet. Diejenigen Flechtgruppen, die sich auf einem
betrachteten Kabelabschnitt auf der Innenseite des Schirms befinden, werden
im folgenden als innere Lage des Schirms bezeichnet. Die Flechtgruppen,
die sich auf diesem Abschnitt auf der Außenseite des Kabelschirms
befinden, bilden die äußere Lage des Schirms.
Das Bild zeigt zur Veranschaulichung
der Geflechtkopplung Längs- und Querschnitt eines geflechtgeschirmten
Kabels, wobei zur vereinfachten Querschnitts-Betrachtung die innere und
die äußere Lage als Hohlzylinder dargestellt sind.
Veranschaulichung der Geflechtkopplung:
a) Kabel-Längsschnitt b) Kabel-Querschnitt
Der gesamte auf dem
Kabelschirm fließende Störstrom I
0 teilt
sich in den Strom der inneren Lage I
si und den Strom
der äußeren Lage I
sa auf. Wie im Bild dargestellt,
induziert das von I
si herrührende Magnetfeld H
i
zwischen dem Innenleiter und der äußeren Lage, die entlang
des Kabels auch zur inneren Lage wird und somit auch einen Teil der Innenseite
des Schirms darstellt, in eine Störspannung U
s
. Im Vergleich mit dem Bild der Aperturkopplung wird deutlich, das die
Umlaufrichtung von H
i um den Mittelleiter zu der für
die Aperturkopplung dargestellten Umlaufrichtung entgegengesetzt ist. Es
handelt sich bei der Geflechtkopplung in der angestellten Betrachtung also
um eine induktive Kopplung mit einer zur Aperturkopplung entgegengesetzten
Phase.
Das erste Modell für
den auf die Geflechtkopplung zurückzuführenden Gegeninduktivitätsbelag
ist:
Hierbei ist D
m
der mittlere Durchmesser des Kabels, h
m der mittlere
Abstand zwischen äußerer und innerer Lage und
a
der Flechtwinkel. Der Faktor a ist unbestimmt und bildet einen Teil des
Korrekturterms zur Berücksichtigung der Feldschwächung von H
i
durch die in die äußere Lage induzierten Ströme.
Die Aufzählung,
Kurzfassung und eventuelle Bewertung aller Publikationen, die die experimentelle
Verifikation der Existenz der Geflechtkopplung zum Inhalt haben, würde
den Rahmen dieser Arbeit sprengen. Wegen der teilweise unbefriedigenden
Übereinstimmung zwischen den publizierten Meßdaten und der angegebenen
Gleichung existiert eine Vielzahl von (semi-) analytischen Modellen.
Definition der komplexen Transferadmittanz
Durch Feldeinfall oder
andere Interferenzen in der Umgebung eines Kabels kann auch eine Störspannung
zwischen dem Kabelschirm und der Umgebung entstehen. Diese Störspannung
hat einen Störstrom auf dem (den) Innenleiter(n) des Kabels zur Folge.
Die diese Einkopplung beschreibende Größe ist die Transferadmittanz
Y'
T .
Schematische Darstellung
zur Definition der Transferadmittanz
Die Transferadmittanz
eines Koaxialkabels ist als längengezogene, komplexe Größe
definiert als das Verhältnis des Störstroms auf dem Innenleiter
I zu der Störspannung auf dem Kabelschirm U
0 ,
wobei die Spannung zwischen Innenleiter und Kabelschirm Null ist.
Die Definition der Transferadmittanz
setzt eine über die Kabellänge l homogene Spannungsverteilung
auf dem Schirm voraus. Die Leitungslänge muß also klein gegenüber
der Wellenlänge sein. Bei einer leitungstheoretischen Simulationsrechnung
oder Meßdatenauswertung ist die differentielle Definition der Transferadmittanz
von Vorteil:
Weiterhin muß
die Spannung U
0 definiert bleiben, der Abstand zwischen
Kabel und Umgebung muß also klein gegenüber der Wellenlänge
sein.
Aperturkopplung
Der wirksame Mechanismus
dieser kapazitiven Einkopplung ist die Aperturkopplung. Das Bild zeigt
schematisch den Verlauf der elektrischen Feldlinien, die durch eine Apertur
des vereinfacht als Hohlzylinder dargestellten Kabelschirms hindurchgreifen.
Schematische Darstellungen
zur Aperturkopplung:
a) Verlauf der elektrischen Feldlinien
b) Kapazitätsbeläge und Geometrie
Der den elektrischen
Felddurchgriff beschreibenden Kapazitätsbelag C'
T
einer
einzelnen Apertur des Radiuses r
0
wird unter der Voraussetzung
C'
T
<<C' in für ein radialsymetrisches Feld hergeleitetet
als:
Hierbei repräsentiert
C' den Kapazitätsbelag zwischen Innenleiter und Kabelschirm, C'
0
den Kapazitätsbelag zwischen Schirm und Umgebung sowie r
a
den Schirmradius.
Für Koaxialkabel
deren Isolation des Innenleiters gegen den Schirm eine relative Permittivität
e
r1
ungleich eins aufweißt,
sowie zur Berücksichtigung der effektiven relativen Permittivität
im Bereich zwischen dem Kabelschirm und der leitfähigen Umgebung
e
r2
wird
der Korrekturfaktor g vorgeschlagen
Der Einfluß mehrerer
Aperturen überlagert sich linear. Stellt
n
die Anzahl der Aperturen pro Längeneinheit dar, kann die Transferadmittanz
als
Es wird deutlich, daß
die Transferadmittanz keine reine Kabelkenngröße ist, da
sie von der Kapazität
des Systems, das von dem Kabelschirm und der leitfähigen Umgebung
gebildet wird, abhängt.
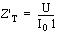
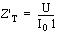
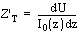
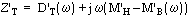
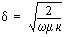
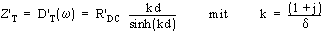

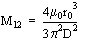 ,
,